This part provides an Integer Linear Programming (ILP) model of the proposed benchmark. It was modeled a flexible job shop problem (FJSP) as close as possible to reality as it contains original constraints from the manufacturing environment. In fact, the ILP resolve the machine allocation at the scheduling problem. This model can be improved by the community or used to compare with meta-heuristics designed by the researchers. It is free of use and can be downloaded here.

If used, please cite the following article: "ORCA-FMS: a dynamic architecture for the optimized and reactive control of flexible manufacturing scheduling" in Computer in Industry, 65(4), 706-720 (Pach, Berger, Bonte, &Trentesaux, 2014)".

Notations for parameters

Notations for variables

Objective function:

Minimize C_max

Details of the constraints:

C_maxcalculation constraint

Define C_max as being at least equal to the last operation completed in the cell.

Precedence constraints

The first constraint (2) ensures that a job operation can only begin if the previous operation for the same job has been completed. If the two operations are not performed on the same machine, a transportation time is taken into consideration. The second constraint (3) ensures that an operation on a machine can only begin if the previous operation performed by this machine has been completed.

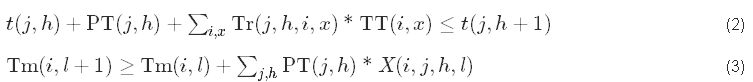
Transportation constraint

If successive job operations are performed on different machines, there is a transportation time between those two operations.

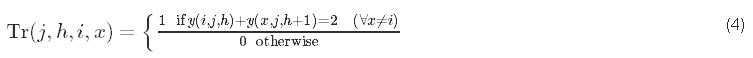
Allocation constraints

These constraints ensure that an operation can only be allocated to a machine that can perform it (5), that only one operation is performed at the same time on one machine (6), and that each operation is allocated to only one machine ((7) and (8)).

Link constraints

These constraints are the link between the variables: operation/job starting time and operation/machine starting time ((9) and (10)); and the link between the allocation of operations to machines and the order in which the operations are processed by the machines (11)

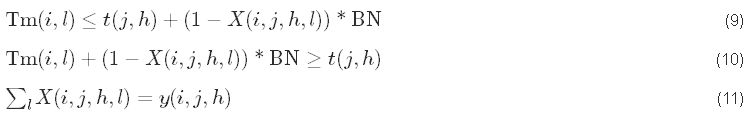
Job limitation constraints

These constraints limit the number of simultaneous jobs in the shop floor according to MJ. O_0j defines the first operation of job j, and O_uj defines the last one. The first constraint (12) defines if an operation is done before another one. The other constraints ((13)–(16)) allow simultaneous jobs in the shop floor to be calculated.

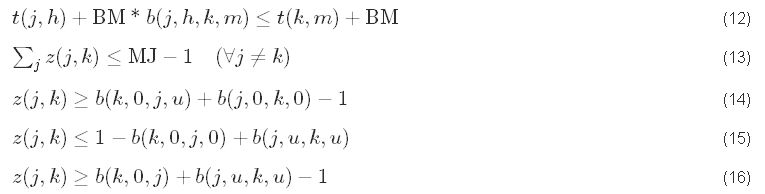
ILP model in CPLEX

You can download the ILP model from the following link: ILP.cs

Components needed:

• Install IBM ILOG CPLEX Optimization Studio (free of charge for education).
• Download the CPLEX concert libraries that are included in the start of the C# program.
• Install a c# environment such as Microsoft Visual C# Studio express

Defining a scenario (within the ILP Model code)

• Set the number of jobs:  Nb_Job (line 32)
• Set the number of places: Nb_place (line 32). It corresponds to the number of operations that can be provided by each resource during the scenario.
• Set the jobs to perform (matrix line 34)
• Choose the Cplex research mode (feasibility, balanced or optimality) (line 43).
• Choose the time limit in seconds (line 44).
• Choose the transportation times (actual times = matrix line 46, neglicted times = line 53)

Getting the results

The C# program provides all the data in the results windows. You will have the starting time of each operation of each the product and the resource associated.